ПРИЛОЖЕНИЕ 18* Обязательное

РАСЧЕТ ОРТОТРОПНОЙ ПЛИТЫ ПРОЕЗЖЕЙ ЧАСТИ ПО ПРОЧНОСТИ И УСТОЙЧИВОСТИ

1. Метод расчета ортотропной плиты должен учитывать совместную работу листа настила, подкрепляющих его ребер и главных балок.

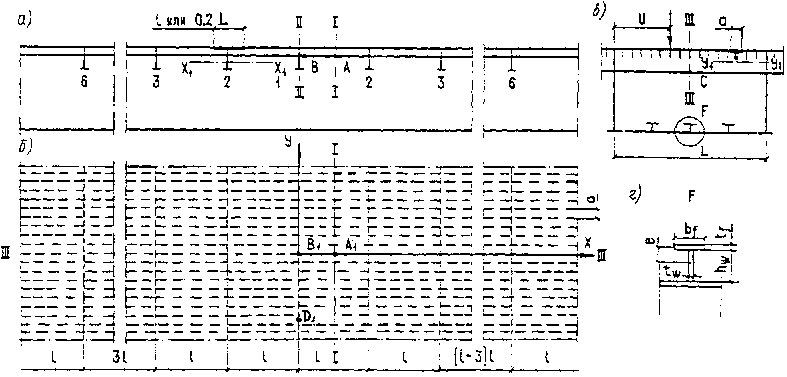
2. Ортотропную плиту допускается условно разделять на отдельные системы – продольные и поперечные ребра с соответствующими участками листа настила (см. чертеж).

Коробчатое пролетное строение

а – продольный разрез; б – план; в – поперечный разрез; г – ребро нижней плиты; 1, 2, 3, ... i – номер поперечного ребра верхней плиты

УСИЛИЯ В ОРТОТРОПНОЙ ПЛИТЕ ПРИ РАБОТЕ НА ИЗГИБ МЕЖДУ ГЛАВНЫМИ БАЛКАМИ

3. Изгибающие моменты в продольных ребрах ортотропной плиты следует определять по формуле

М_si = М₁ + М, (1)

M₁ – изгибающий момент в отдельном продольном ребре полного сечения, включающего прилегающие участки листа настила общей шириной, равной расстоянию а между продольными ребрами (см. чертеж, в), рассматриваемом как неразрезная балка на жестких опорах; момент определяется от нагрузки, расположенной непосредственно над этим ребром;

М – изгибающий момент в опорном сечении продольного ребра при изгибе ортотропной плиты между главными балками, определяемый при загружении поверхности влияния нагрузкой, прикладываемой в узлах пересечения продольных и поперечных ребер.

Нагрузку, передаваемую с продольных ребер на узлы пересечения с поперечными ребрами, следует определять с помощью линии влияния опорной реакции неразрезной многопролетной балки на жестких опорах.

В пределах крайних третей ширины ортотропной плиты автопроезда и в ортотропной плите однопутных железнодорожных пролетных строений с ездой поверху следует принимать М = 0.

Ординаты поверхности влияния для вычисления изгибающего момента М в опорном сечении продольного ребра над “средним” поперечным ребром l (см. чертеж, а) следует определять по формуле

, (2)*

где M_1i - принимаемые по табл. 1 (с умножением на l) ординаты линии влияния изгибающего момента в опорном сечении продольного ребра над “средним” поперечным ребром l при расположении нагрузки над поперечным ребром i;

l – пролет продольного ребра (см. чертеж, б);

L – пролет поперечного ребра (см. чертеж, в);

u – координата положения нагрузки от начала поперечного ребра.

Таблица 1

Номер поперечного ребра i	Ординаты линии влиянияпри z
	0	0,1	0,	0,5	1,0
1	0	0,0507	0,0801	0,1305	0,1757
2	0	-0,0281	-0,0400	-0,0516	-0,0521
3	0	0,0025	-0,0016	-0,0166	-0,0348
4	0	0,0003	0,0016	0,0015	0,0046
5	0	-0,0001	0	0,0014	0,0025
6	0	0	0	0,0001	0,0012

В табл. 1 обозначено:

z - параметр, характеризующий изгибную жесткость ортотропной плиты и определяемый по формуле

,

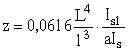где I_sl - момент инерции полного сечения продольного ребра относительно горизонтальной оси (см. чертеж в);

a - расстояние между продольными ребрами;

I_s - момент инерции полного поперечного ребра – с прилегающим участком настила шириной 0,2 L, но не более l – относительно горизонтальной оси х₁ (см. чертеж, а).

Примечание. В табл. 1 принята следующая нумерация поперечных ребер i: ребра 2–6 расположены на расстоянии l одно от другого в каждую сторону от “среднего” поперечного ребра 1 (см. чертеж, a).

4. В железнодорожных пролетных строениях лист настила ортотропной плиты проезжей части следует рассчитывать на изгиб, при этом прогиб листа настила не проверяется.

При устройстве пути на балласте наибольшие значения изгибающих моментов в листе настила над продольными ребрами следует определять по формулам:

в зоне под рельсом

M_y = -0,1 n a² ; (3)

в зоне по оси пролетного строения

M_y = -0,08 n a² , (4)

где n – нагрузка на единицу длины, принимаемая по п. 2 обязательного приложения 5*.

РАСЧЕТ ЭЛЕМЕНТОВ ОРТОТРОПНОЙ ПЛИТЫ ПО ПРОЧНОСТИ

5. Для проверки прочности элементов ортотропной плиты необходимо получить в результате расчетов в предположении упругих деформаций, стали в сечениях I, II, III и точках А, В, С, А₁, В₁, D₁, указанных на чертеже, нормальные напряжения в листе настила, продольных и поперечных ребрах, а также касательные напряжения в листе настила, от изгиба ортотропной плиты между главными балками s _xp, s _yp и t _xyp и совместной работы ее с главными балками пролетного строения s _xc, s _yc и t _xyc.

6. Проверку прочности растянутого при изгибе ортотропной плиты крайнего нижнего волокна продольного ребра следует выполнять в зоне отрицательных моментов неразрезных главных балок в сечении I–I посредине пролета l среднего продольного ребра (см. чертеж, а – точка A) по формулам:

y s _xc + m_{1c 1s xp}Ј R_y m ; (5)

s _xc + s _xpЈ m₂ R_yn m , (6)

где R_y, R_yn – расчетное и нормативное сопротивления металла продольного ребра;

m – коэффициент условий работы, принимаемый по табл. 60*;

m₁, m₂ – коэффициенты условий работы; для автодорожных и городских мостов, а также для автодорожного проезда совмещенных мостов их следует принимать по табл. 2*; для железнодорожных и пешеходных мостов, а также для железнодорожного проезда совмещенных мостов

; при этом проверка по формуле (6) не выполняется;

c – коэффициент влияния собственных остаточных напряжений, принимаемый c ₁ = 0,9 – для крайнего нижнего волокна продольного ребра, выполненного из полосы, прокатного уголка или прокатного тавра, и c ₁ = 1,1 – для продольного ребра в виде сварного тавра;

,

y , – коэффициенты, определяемые по пп. 4.28* и 4.26*.

Таблица 2*

s xc / s xp	Значения коэффициентов m1 и m2 для полосовых ребер
	m1	m2
0	0,55	1,40
0,25	0,40	1,50
0,45	0,25	1,60
0,65	0,13	1,60

Примечание. Коэффициенты m₁ и m₂ для промежуточных значений s _xc/s _xp следует определять линейной интерполяцией.

7. Проверку прочности сжатого при местном изгибе ортотропной плиты крайнего нижнего волокна продольного ребра следует выполнять в зоне положительных моментов неразрезных главных балок в опорном сечении II–III среднего продольного ребра (см. чертеж а – точка В) по формуле

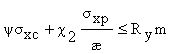,(7)

где

, y – коэффициенты, определяемые по пп. 4.28* и 4.26*;

c ₂ - коэффициент влияния собственных остаточных напряжений, принимаемый c ₂ = 1,1 – для крайнего нижнего волокна ребра, выполненного из полосы, прокатного уголка или прокатного тавра, и c ₂ = 0,9 – для ребра в виде сварного тавра;

m - коэффициент условий работы, принимаемый по табл. 60*.

8. Проверку прочности крайнего нижнего волокна поперечной балки следует выполнять в сечении III–III посредине ее пролета (см. чертеж в – точка С) по формуле

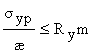(8)

где

– коэффициент, определяемый по формулам (143) и (144);

m – коэффициент условий работы, принимаемый по табл. 60*.

9. Расчет по прочности листа настила следует выполнять в точках А₁, В₁, D₁ (см. чертеж б) по формулам:

; (9)

t _xyЈ R_s m , (10)

гдеs _x = s _xc + m₄s _xp ; s _y = s _yc + m₄s _yp ;

t _xy = t _xyc + t _xyp ;

m - коэффициент условий работы, принимаемый по табл. 60*;

m₃ – коэффициент, равный 1,15 при s _y = 0 или 1,10 при s _y№ 0;

m₄ – коэффициент условий работы, принимаемый равным 1,05 – при проверке прочности листа настила в точке A₁ ортотропной плиты автодорожных и городских мостов и 1,0 – во всех остальных случаях.

При выполнении данной проверки допускается принимать в качестве расчетных загружения, при которых достигает максимального значения одно из действующих в данной точке ортотропной плиты напряжений s _x, s _y или t _xy.

РАСЧЕТ ЭЛЕМЕНТОВ ОРТОТРОПНОЙ ПЛИТЫ ПО УСТОЙЧИВОСТИ

10. Местная устойчивость листа настила между продольными ребрами, продольных полосовых ребер, свесов поясов тавровых продольных и поперечных ребер должна быть обеспечена согласно пп. 4.45* и 4.47, а стенки тавровых ребер – согласно обязательному приложению 16*. При этом следует выбирать наиболее невыгодную комбинацию напряжений от изгиба ортотропной плиты между главными балками и совместной ее работы с главными балками пролетного строения.

11. Общая устойчивость листа настила, подкрепленного продольными ребрами, должна быть обеспечена поперечными ребрами.

Момент инерции поперечных ребер J_s (см. п. 3) сжатой (сжато-изогнутой) ортотропной плиты следует определять по формуле

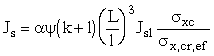, (11)*

где a – коэффициент, определяемый по табл. 2, а*;

y – коэффициент, принимаемый равным: 0,055 при k = 1; 0,15 при k = 2; 0,20 при k і 3;

k – число продольных ребер рассчитываемой ортотропной плиты;

L – расстояние между стенками главных балок или центрами узлов геометрически неизменяемых поперечных связей;

l – расстояние между поперечными ребрами;

J_sl – момент инерции полного сечения продольного ребра (см. п. 3);

s _xc – действующие напряжения в листе настила от совместной работы ортотропной плиты с главными балками пролетного строения, вычисленные в предположении упругих деформаций стали;

s _x,cr,ef – напряжение, вычисленное по табл. 68* по значению s _x,cr = s _xc.

Таблица 2а*

w	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	0,95	1
a	0	0,016	0,053	0,115	0,205	0,320	0,462	0,646	0,872	1,192	1,470	2,025

Допускается также определять s _x,cr,ef по следующей формуле

.

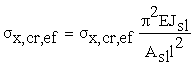
Примечание. Коэффициент w определяется по формуле

, где j ₀ следует находить по табл. 3* п. 12 при l_ef = l.

Для сжатой ортотропной плиты, не воспринимающей местной нагрузки, в формуле (11)* коэффициент a следует принимать равным 2,025, что обеспечивает равенство расчетной длины l_ef продольных ребер расстоянию между поперечными ребрами l.

12*. Расчет по общей устойчивости ортотропной плиты в целом (сжатой и сжато-изогнутой) при обеспечении условия (11)* следует выполнять по формуле

s _xcЈ j ₀ R_y m , (12)*

где s _xc – см. п. 11*;

j ₀ – коэффициент продольного изгиба, принимаемый по табл. 3* в зависимости от гибкости l ₀;

m – коэффициент условий работы, принимаемый по табл. 60* п. 4.19*.

Таблица 3*

Гибкость l 0, l 1	Коэффициент j 0 для стали марок
	16Д	15ХСНД	10ХСНД, 390-14Г2АФД, 390-15Г2АФДпс
0	1,00	1,00	1,00
41	1,00	1,00	1,00
44	1,00	1,00	0,96
50	1,00	0,92	0,88
53	1,00	0,87	0,83
60	0,95	0,76	0,72
70	0,83	0,64	0,59
80	0,73	0,56	0,49
90	0,64	0,50	0,43
100	0,59	0,44	0,38
110	0,53	0,39	0,33
120	0,47	0,34	0,28
130	0,41	0,30	0,25
140	0,36	0,26	0,22
150	0,32	0,23	0,20
160	0,29	0,21	0,17
170	0,26	0,19	0,16
180	0,23	0,17	0,14
190	0,21	0,15	0,13
200	0,20	0,14	0,11

Гибкость следует определять по формуле

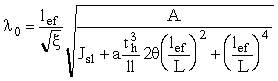, (13)*

где l_ef - расчетная (свободная) длина продольных ребер, определяемая из выражения

.

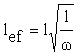Коэффициент w находят из табл. 2а* по значению

;

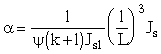J_s , J_sl и l - см. п. 3;

a - расстояние между продольными ребрами;

l_h - толщина листа настила;

x - коэффициент, принимаемый равным 1,0 –для ортотропной плиты нижнего пояса и по табл. 4* – для плиты верхнего пояса коробчатых главных балок;

A - площадь полного сечения продольного ребра;

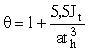- (здесь J_t – момент инерции полного сечения продольного ребра при чистом кручении).

Таблица 4*

f / i	Коэффициент x
0	1,00
0,01	0,75
0,05	0,70
0,10	0,66

f – прогиб продольного ребра между поперечными ребрами;

i – радиус инерции полного сечения продольного ребра.

Сжато-изогнутую ортотропную плиту железнодорожных мостов на общую устойчивость следует проверять по формуле (167), принимая гибкость по формуле (13)* при x = 1,0.

13. Тавровые продольные ребра (см. чертежи, в, г) сжатой ортотропной плиты нижнего пояса коробчатых главных балок при изгибно-крутильной форме потери устойчивости следует рассчитывать по формуле (12)*, принимая коэффициент продольного изгиба j ₀ в зависимости от гибкости l ₁.

Гибкость l ₁ следует определять по формуле

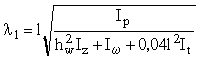, (14)

где I_p = I_y + I_z + A (h_w - e)² ;

l – см. п. 3;

h_w – высота стенки ребра толщиной t_w (см. чертеж, г);

е – расстояние от центра тяжести полки шириной b_f, толщиной t_f до центра тяжести таврового продольного ребра (см. чертеж, г);

I_y, I_z – соответственно момент инерции сечения таврового продольного ребра относительно горизонтальной оси у и вертикальной оси z;

;

;

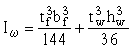A = b_f t_f + h_w t_w .

Для обеспечения местной устойчивости элементов таврового сечения продольного ребра толщина полки и стенки должна удовлетворять требованиям п. 4.45*:

при b_f > 0,3 h_w продольное ребро полного сечения следует считать двутавром, при b_f = 0 – тавром;

при 0 < b_fЈ 0,3 h_w требования к толщине стенки определяются по линейной интерполяции между нормами для двутавра и тавра (b_f = 0).