ПРИЛОЖЕНИЕ 16* Обязательное

РАСЧЕТ ПО УСТОЙЧИВОСТИ ПОЛОК И СТЕНОК ЭЛЕМЕНТОВ, ПОДКРЕПЛЕННЫХ РЕБРАМИ ЖЕСТКОСТИ

1. Прямоугольные отсеки полок и стенок (далее – пластинки), заключенные между подкрепляющими их по контуру ортогональными деталями (ребра жесткости, полка для стенки и стенка для полки), следует рассчитывать по устойчивости. При этом расчетными размерами и параметрами проверяемой пластинки являются:

а – длина пластинки, равная расстоянию между осями поперечных ребер жесткости;

h_ef – расчетная ширина пластинки, равная:

при отсутствии продольных ребер жесткости у прокатного или сварного элемента – расстоянию между осями поясов h_w или осями стенок коробчатого сечения b_f;

то же, у составного элемента с болтовыми соединениями – расстоянию между ближайшими рисками поясных уголков;

при наличии продольных ребер жесткости у сварного или прокатного элемента – расстоянию от оси пояса (стенки) до оси крайнего продольного ребра жесткости h₁ и h_n или расстоянию между осями соседних продольных ребер жесткости h_i (i = 2; 3; 4; 5...);

то же, у составного элемента с болтовыми соединениями – расстоянию от оси крайнего ребра жесткости до ближайшей риски поясного уголка h₁ и h_n или расстоянию между осями соседних продольных ребер жесткости h_i (i = 2; 3; 4; 5...);

t – толщина проверяемой пластинки;

t₁, b₁ – толщина и расчетная ширина листа, ортогонального к проверяемой пластинке; в расчетную ширину этого листа в двутавровом сечении следует включать (в каждую сторону от проверяемой пластинки) участок листа шириной z ₁t₁, но не более ширины свеса, а в коробчатом сечении – участок шириной 1/2 z ₂t₁, но не более половины расстояния между стенками коробки (здесь коэффициенты z ₁ и z ₂ следует определять по п. 4.55*);

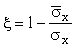; здесь s _x и

`s_x   определяются по п. 2;

;

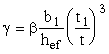; здесь b – коэффициент, принимаемый по табл. 1.

Таблица 1

Характер закрепления сжатого пояса конструкцией проезжей части	Значение коэффициента b
К поясу с помощью лапчатых болтов прикреплены мостовые брусья	0,3
К поясу с помощью высокопрочных шпилек и деревянных подкладок прикреплены сборные железобетонные плиты проезжей части	0,5
Пояс свободен	0,8
К поясу приварен внахлестку или встык лист ортотропной плиты	2,0
К поясу с помощью закладных деталей и высокопрочных болтов присоединена сборная проезжая часть сталежелезобетонного пролетного строения	1,5
К поясу непрерывно по всей длине пролета присоединена проезжая часть сталежелезобетонного пролетного строения с помощью высокопрочных болтов и подливки цементно-песчаным раствором	20

В случае если проверяемая пластинка примыкает к пакету из двух и более листов, за t₁ и b₁ принимаются толщина и расчетная ширина первого листа пакета, непосредственно примыкающего к указанной пластинке.

2. Расчет по устойчивости пластинок следует выполнять с учетом всех компонентов напряженного состояния – s _x, s _y, t _xy .

Напряжения s _x, s _y, t _xy следует вычислять в предположении упругой работы материала по сечению брутто без учета коэффициентов продольного изгиба.

Максимальное s _x и минимальное `s_x продольные нормальные напряжения (положительные при сжатии) по продольным границам пластинки следует определять по формулам:

;

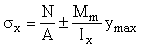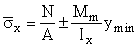, (1)

где

y_max, y_min - максимальное и минимальное расстояния от нейтральной оси до продольной границы пластинки (с учетом знака);

M_m - среднее значение изгибающего момента в пределах отсека при m Ј 1; если длина отсека больше его расчетной ширины, то М_m следует вычислять для более напряженного участка длиной, равной ширине отсека; если в пределах отсека момент меняет знак, то М_m следует вычислять на участке отсека с моментом одного знака.

Среднее касательное напряжение t _xy следует определять:

при отсутствии продольных ребер жесткости – по формуле

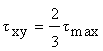, (2)

где

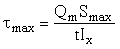; (3)

при их наличии – по формуле

. (4)

В формулах (3) и (4):

Q_m – среднее значение поперечной силы в пределах отсека, определяемое так же, как M_m;

t ₁, t ₂ – значения касательных напряжений на продольных границах пластинки, определяемые по формуле (3) при замене S_max соответствующими значениями S.

Поперечное нормальное напряжение s _y (положительное при сжатии), действующее на внешнюю кромку крайней пластинки, следует определять:

от подвижной нагрузки – по формуле

, (5)

где Р – распределенное давление на внешнюю кромку крайней пластинки, определяемое по обязательному приложению 5*;

от сосредоточенного давления силы F – по формуле

, (6)

где l_ef – условная длина распределения нагрузки.

Условную длину распределения нагрузки l_ef следует определять:

при передаче нагрузки непосредственно через пояс балки или через рельс и пояс – по формуле

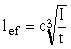, (7)

где с – коэффициент, принимаемый для сварных и прокатных элементов равным 3,25, для элементов с соединениями на высокопрочных болтах – 3,75, на обычных болтах – 4,5;

I – момент инерции пояса балки или сумма моментов инерции пояса и рельса;

при передаче нагрузки от катка через рельс, деревянный лежень и пояс балки l_ef следует принимать равной 2h (где h – расстояние от поверхности рельса до кромки пластинки), но не более расстояния между соседними катками.

Поперечные нормальные напряжения s _y на границе второй и последующих пластинок следует определять, как правило, по теории упругости.

Допускается их определять:

при нагрузке, распределенной по всей длине пластинки, – по формуле

; (8)

при сосредоточенной нагрузке – по формуле

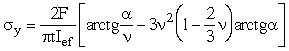. (9)

В формулах (8) и (9):

;

,

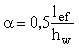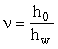где h₀ – часть высоты стенки, равная расстоянию от оси нагруженного пояса в сварных и прокатных балках или от ближайшей риски поясного уголка в балках с болтовыми соединениями до границы проверяемой пластинки;

h_w – полная высота стенки.

3. Критические напряжения s _x,cr , s _y,cr , t _xy,cr , s _x,cr,ef , s _y,cr,ef , t _xy,cr,ef следует определять в предположении действия только одного из рассматриваемых напряжений s _x , s _y или t _xy. Приведенные критические напряжения s _x,cr,ef , s _y,cr,ef , t _xy,cr,ef общем случае вычисляют в предположении неограниченной упругости материала на основе теории устойчивости первого рода (бифуркация форм равновесия) для пластинчатых систем.

Значения приводимых в табл. 2, 4–13 параметров для определения критических напряжений в пластинках допускается находить по линейной интерполяции.

4. Расчет по устойчивости стенки сплошных изгибаемых элементов, имеющей только поперечные ребра жесткости, следует выполнять по формуле

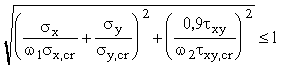, (10)

где s _x,cr , s _y,cr - критические нормальные напряжения соответственно продольное и поперечное;

t _xy,cr – критическое касательное напряжение;

w ₁ – коэффициент, принимаемый по табл. 2;

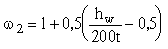- коэффициент, вводимый при расчете автодорожных и городских мостов при h_ц / t > 100.

Таблица 2

x	0	0,5	1,0	1,5	2,0	3,0	4,0
w 1	1,00	1,05	1,10	1,15	1,20	1,30	1,40

Критические напряжения s _x,cr , s _y,cr , t _xy,cr следует определять по формулам табл. 3* в зависимости от приведенных критических напряжений s _x,cr,ef , s _y,cr,ef , t _xy,cr,ef , вычисляемых по пп. 4.1–4.3 настоящего приложения. При этом t _xy,cr определяется по формулам для s _x,cr с подстановкой в них соотношений:

;

.

Таблица 3*

Марка стали	Интервал значений s x,cr,ef, МПа (кгс/см2)	Формулы* для определения s x,cr и s y,cr
16Д	0-196 (0-2000)	s x,cr = 0,9s x,cr,efm
	196-385 (2000-3921)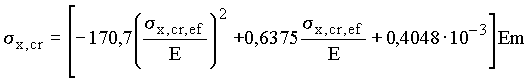
	Св. 385 (cв. 3921)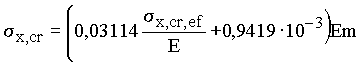
15ХСНД	0-207 (0-2111)	s x,cr = 0,9s x,cr,efm
	207-524 (2111-5342)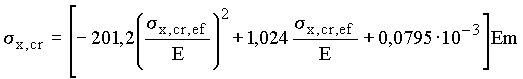
	Св. 524 (св. 5342)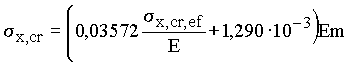
10ХСНД 390-14Г2АФД 390-15Г2АФДпс	0-229 (0-2333)	s x,cr = 0,9s x,cr,efm
	229-591 (2333-6024)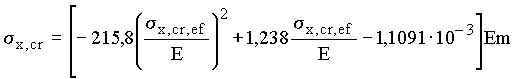
	Св. 591 (св. 6024)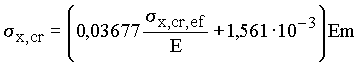

_________
* При определении поперечных нормальных критических напряжений в формулах заменяются s _x,cr на s _y,cr и s _x,cr,ef на s _y,cr,ef. Здесь m - коэффициент условий работы, принимаемый по табл.60*.

4.1. Приведенное критическое продольное нормальное напряжение для пластинок стенки изгибаемого элемента следует определять по формуле

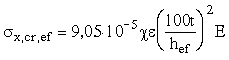, (11)

где c - коэффициент упругого защемления стенки, принимаемый для элементов с болтовыми соединениями равным 1,4, для сварных элементов – по табл. 4;

e - коэффициент, принимаемый по табл. 5.

Таблица 4

g	0,25	0,5	1,0	2,0	4,0	10,0	Св. 10
c	1,21	1,33	1,46	1,55	1,60	1,63	1,65

Таблица 5

x	Значение коэффициента e при m
	0,4	0,5	0,6	0,67	0,75	0,8	0,9	1,0	1,5	2 и более
0	8,41	6,25	5,14	4,75	4,36	4,2	4,04	4,0	4,34	4,0
0,67	10,8	8,0	7,1	6,6	6,1	6,0	5,9	5,8	6,1	5,8
0,80	13,3	9,6	8,3	7,7	7,1	6,9	6,7	6,6	7,1	6,6
1,00	15,1	11,0	9,7	9,0	8,4	8,1	7,9	7,8	8,4	7,8
1,33	18,7	14,2	12,9	12,0	11,0	11,2	11,1	11,0	11,5	11,0
2,00	29,1	25,6	24,1	23,9	24,1	24,4	25,6	25,6	24,1	23,9
3,00	54,3	54,5	58,0	53,8	53,8	53,8	53,8	53,8	53,8	53,8
4,00	95,7	95,7	95,7	95,7	95,7	95,7	95,7	95,7	95,7	95,7

4.2. Приведенное критическое поперечное нормальное напряжение s _y,cr,ef для пластинок стенки изгибаемого элемента следует определять по формуле

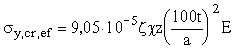, (12)

где z – коэффициент, принимаемый равным единице при нагрузке, распределенной по всей длине пластинки, и по табл. 6 – при сосредоточенной нагрузке;

c – коэффициент упругого защемления стенки, принимаемый по табл. 7;

z - коэффициент, принимаемый по табл. 8.

Таблица 6

m	Значения коэффициентов z при r
	0,10	0,11	0,12	0,13	0,14	0,15	0,16	0,18	0,20	0,25	0,30	0,35
0,5	1,70	1,67	1,65	1,63	1,61	1,60	1,60	1,60	1,60	1,60	1,60	1,60
0,6	1,98	1,93	1,89	1,85	1,82	1,80	1,79	1,78	1,76	1,72	1,71	1,69
0,7	2,23	2,17	2,11	2,06	2,02	1,98	1,96	1,93	1,89	1,82	1,79	1,76
0,8	2,43	2,35	2,28	2,22	2,17	2,12	2,10	2,05	2,01	1,91	1,86	1,82
0,9	2,61	2,51	2,43	2,36	2,30	2,24	2,21	2,16	2,11	1,98	1,92	1,87
1,0	2,74	2,64	2,55	2,47	2,40	2,34	2,31	2,24	2,17	2,04	1,97	1,91
1,2	2,79	2,68	2,59	2,51	2,43	2,37	2,33	2,26	2,19	2,05	1,98	1,91
1,4	2,84	2,73	2,63	2,54	2,46	2,39	2,35	2,28	2,21	2,05	1,98	1,91
1,5	2,86	2,75	2,65	2,56	2,48	2,41	2,37	2,30	2,22	2,07	1,99	1,91
2,0 и более	2,86	2,75	2,65	2,55	2,47	2,40	2,36	2,28	2,20	2,05	1,96	1,88

Таблица 7

g	Значение коэффициента c при m
	0,4	0,6	0,8	1,0	1,5	2,0 и более
0,25	1,19	1,19	1,20	1,20	1,19	1,18
0,5	1,24	1,29	1,30	1,32	1,32	1,32
1,0	1,28	1,36	1,41	1,47	1,52	1,56
4,0	1,32	1,45	1,57	1,73	1,97	2,21
10 и более	1,34	1,49	1,65	1,88	2,51	2,95

Таблица 8

m	z
0,4	4,88
0,5	5,12
0,6	5,37
0,7	5,59
0,8	5,80
1,0	6,26
1,2	6,87
1,4	7,69
1,6	8,69
1,8	9,86
2,0	11,21
2,5 и более	15,28

4.3. Приведенное критическое касательное напряжение t _xy,cr,ef для пластинок стенок изгибаемого элемента следует определять по формуле

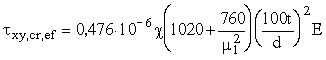, (13)

где d - меньшая сторона отсека (а или h_ef);

m ₁ - коэффициент, принимаемый равным m при a > h_ef и 1/m при a < h_ef;

c - коэффициент упругого защемления стенки, принимаемый равным единице для элементов с болтовыми соединениями и по табл. 9 – для сварных элементов.

Таблица 9

g	Значение коэффициента c при m
	0,5	0,67	1,0	2,0	2,5 и более
0,25	1,014	1,063	1,166	1,170	1,192
0,5	1,016	1,075	1,214	1,260	1,300
1,0	1,017	1,081	1,252	1,358	1,416
2,0	1,018	1,085	1,275	1,481	1,516
5,0	1,018	1,088	1,292	1,496	1,602
10,0	1,018	1,088	1,298	1,524	1,636
Св. 10	1,018	1,089	1,303	1,552	1,580

5. Расчет по устойчивости пластинок стенки сплошных изгибаемых элементов, имеющих поперечные ребра и одно продольное ребро в сжатой зоне, следует выполнять:

первой пластинки – между сжатым поясом и продольным ребром – по формуле

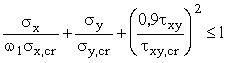, (14)

где w ₁ - коэффициент, принимаемый по табл. 2;

s _x , s _y , t _xy - напряжения, определяемые по п. 2;

s _x,cr, s _y,cr, t _xy,cr критические напряжения, определяемые согласно п. 4;

второй пластинки – между растянутым поясом и продольным ребром – по формуле (10), принимая при этом w ₂ = 1.

5.1. Приведенное критическое продольное нормальное напряжение s _x,cr,ef следует определять по формуле (11), при этом коэффициент упругого защемления следует принимать:

первой пластинки: элементов с болтовыми соединениями – c = 1,3; таких же и сварных элементов при объединении с железобетонной плитой – c = 1,35; прочих сварных элементов – по табл. 10;

второй пластинки – c = 1.

Таблица 10

g	0,5	1,0	2,0	5,0	10 и более
c	1,16	1,22	1,27	1,31	1,35

5.2. Приведенное критическое поперечное нормальное напряжение s _y,cr,ef первой пластинке следует определять по формуле

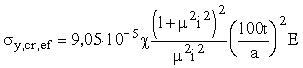, (15)

где i - коэффициент, принимаемый равным 1,0 при

и 2,0 при 0,7 > m > 0,4;

c - коэффициент упругого защемления, принимаемый по табл. 11 для элементов, объединенных с железобетонной плитой, и для балок с болтовыми соединениями, по табл. 12 – для сварных балок.

Таблица 11

m	0,5	0,8	1,0	1,5	2,0 и более
c	1,07	1,18	1,31	1,52	1,62

Таблица 12

g	Значение коэффициента c при m
	0,5	0,6	0,9	1,0	1,5	2,0	2,5	3,0
2	1,06	1,07	1,13	1,17	1,31	1,32	1,29	1,25
4	1,06	1,07	1,14	1,19	1,38	1,44	1,43	1,39

Приведенное критическое поперечное нормальное напряжение s _y,cr,ef при воздействии сосредоточенной нагрузки, когда действующие напряжения определяются по формуле (6), следует вычислять по формуле (15) с умножением на коэффициент 1,55; если при этом а>2h₁+2l_ef, то надлежит принимать:

.

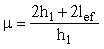Приведенное критическое поперечное нормальное напряжение s _y,cr,ef во второй пластинке следует определять по формуле (12), при этом следует принимать: c = 1; z – по табл. 8; z – по табл. 6 при r = 0,35.

5.3. Приведенное критическое касательное напряжение t _xy,cr,ef следует определять по формуле (13), при этом для первой пластинки вместо коэффициента защемления должен быть принят коэффициент

,

для второй пластинки – c = 1.

6. Расчет по устойчивости пластинок стенки сплошных изгибаемых элементов, имеющих поперечные ребра и несколько продольных ребер жесткости, следует выполнять:

первой пластинки – между сжатым поясом и ближайшим ребром – по формуле (14) и формулам (11), (15) и (13) для s _x,cr,ef, s _y,cr,ef, t _xy,cr,ef соответственно;

для последующих сжатых пластинок – по формулам для первой пластинки, принимая коэффициент защемления c = 1;

для сжато-растянутой пластинки – по формуле (10), принимая w ₁ = 1, и формулам (11), (15) и (13) для s _x,cr,ef, s _y,cr,ef, t _xy,cr,ef как для второй пластинки по п. 5.

Расчет по устойчивости пластинки растянутой зоны стенки следует выполнять по формуле

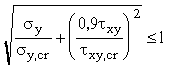, (16)

где

s _y,cr , t _xy,cr - критические поперечное нормальное и касательное напряжения, определяемые по s _y,cr,ef и t _xy,cr,ef согласно указаниям п. 4, при этом приведенное критическое поперечное нормальное напряжение s _y,cr,ef следует определять по формуле

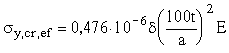, (17)

где d – коэффициент, принимаемый по табл. 13.

Таблица 13

Тип пластинки	Значения коэффициента d при
	0,4	0,5	0,6	0,7	0,8	1,0	1,5	2,0
Примыкающая к растянутому поясу	1240	1380	2520	1650	1820	2240	3860	6300
Промежуточная	920	970	1020	1060	1100	1190	1530	2130

Примечание. а и h_ef следует определять по п. 1.

Приведенное критическое касательное напряжение t _xy,cr,ef следует определять:

для пластинки, примыкающей к растянутому поясу, – по формуле

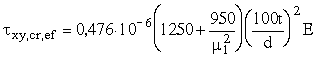, (18)

для промежуточной растянутой пластинки – по формуле

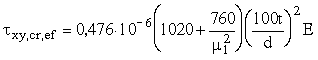, (19)

где d – меньшая сторона отсека (а или h_ef);

m ₁ – коэффициент, принимаемый равным m при а > h_ef и 1/m при а < h_ef .

7. Расчет по устойчивости пластинок стенки сплошных сжато-изгибаемых элементов (балки жесткости пролетного строения распорной системы, арки или пилона) при сжатии сечения по всей высоте следует выполнять по формуле

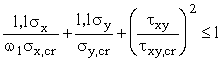, (20)

где s _х – максимальное продольное нормальное напряжение на границе пластинки от продольной силы N и изгибающего момента М_m, принимаемого в соответствии с п. 2;

w ₁ – коэффициент, определяемый по табл. 2;

s _y , s _x – поперечное нормальное и среднее касательное напряжения, определяемые согласно п. 2;

s _x,cr , s _y,cr , t _xy,cr - критические напряжения, определяемые по s _x,cr,ef , s _y,cr,ef , t _xy,cr,ef согласно указаниям п. 4.

При действии на части высоты сечения растягивающих напряжений расчет следует выполнять как для стенки сплошных изгибаемых элементов (см. пп. 4–6).