ГОСТ 10518-88 (Приложение 4)
| ПРИЛОЖЕНИЕ 4 (Обязательное) ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ ДЛЯ ПОЛУЧЕНИЯЗАВИСИМОСТИ МЕЖДУ РЕСУРСОМ И ТЕМПЕРАТУРОЙ 1. Зависимость ресурса от температуры выражают формулой (3), полученной из формулы (2). u = a1 + a2x (3) где u=lgL; x = 1/T a1 = Aў a2 = Bў. 2. Результаты испытаний начинают обрабатывать с вычисления ресурса, полученного при испытаниях каждого образца. Ресурс образцов, которые испытывают в лабораторных камерах тепла и у которых приложение воздействия производят после извлечения образцов из камеры, вычисляют в часах как суммарное время воздействия испытательной температуры во всех циклах испытаний за вычетом половины длительности воздействия в последнем цикле, после которого наступил отказ образцов. Половину длительности не вычитают, если методика определения параметров образца позволяет определить момент наступления отказа в процессе воздействия температуры (например, при испытаниях путем работы под током, при этом время воздействие испытательной температуры считают с момента включения образцов до момента отключения). 3. После того как все образцы отказали, вычисляют ресурс при каждой испытательной температуре. Для предварительной оценки при испытаниях при наименьшей испытательной температуре допускается принимать значение ресурса 50 %-ного образца. Для предварительной оценки результатов испытаний вычисляют средний ресурс как среднее арифметическое ресурсов всех образцов, испытывавшихся в данном режиме. После этого вычисляют логарифмы каждого ресурса ui и среднелогарифмический ресурс в каждом испытательном режиме (среднее арифметическое логарифмов ресурсов) ` uic
где nic - число образцов, испытывавшихся в каждом испытательном режиме. 4. При необходимости затем результаты испытаний корректируют, исключая из рассмотрения образцы с резко выделяющимися значениями логарифмов ресурсов, согласно приложению 5. Для каждого испытательного режима вычисляют среднелогарифмический корректированный ресурс (среднее арифметическое логарифмов ресурсов всех оставшихся для рассмотрения образцов) ` ui,. 5. Следующим этапом обработки данных является вычисление коэффициентов формулы (3). Сначала определяют средние значения ` uxk и ` xik
где nxi - число испытательных режимов (число значений температур); ` xik - значения ` х для каждой температуры испытаний; ui -корректированный среднелогарифмический ресурс при каждой температуре испытаний:
а1 = ` uxk – a2`хik (8) При испытаниях готовых изделий путем работы под током в тех случаях, когда фактические температуры обмоток, испытывавшихся при одинаковой номинальной испытательной температуре, различаются более чем на 3°С, коэффициент а2' определяют по формуле
где N - общее число оставшихся для рассмотрения образцов во всех испытательных режимах испытаний; х - величина х для каждого образца;
6. Определяют дисперсии ресурсов u. 6.1. Вычисляют дисперсию для каждого испытательного режима
где ni - число образцов, оставленных для рассмотрения в каждом испытатели- ном режима. Если в случае измерения параметров-критериев отказа в конце цикла или в конце заданного - интервала времени между измерениями (далее - цикла) все отказы в каком-либо из режимов произошли только в одном или двух циклам, то дисперсию данного режима 6.2. Вычисляют средневзвешенную дисперсию
где fi = ni - 1 (степень свободы данного режима);
6.3 Проводят проверку гипотезы однородности дисперсий. Проверку проводят с использованием критерия Барлета в соответствии с ГОСТ 21126-75. 6.4 Вычисляют дисперсию
Число степеней свободы здесь f3k = nxi –2. 6.5 Вычисляют общую дисперсию, то есть дисперсию всех экспериментальных точек относительно вычисленной линии регрессии (формула 3 коэффициенты а1 и а2 соответственно по формулам 8 или 11 и 7 или 9)
где fs = N - 2 6.6 Вычисляют дисперсию средних значений линии регрессии (дисперсию, характеризующую возможное смещение генерального cpеднегo относительно линии регрессии, которая вычислена по выборочным данным)
где хi - значение х при требуемой температуре. 7 Проводят проверку гипотезы линейности. Вычисляют дисперсионное отношение F
Сравнивая это дисперсионное отношение F с Fтабл для необходимого уровня значимости, принимают или отвергают гипотезу линейности в соответствии с требованиями ГОСТ 21126-75 (приложение 5). 8. Определяют вид статистического распределения экспериментальных данных (логарифмически-нормальное распределение или распределение Вейбулла) в соответствии с ГОСТ 11.008-75 или ГОСТ 11.006-74 или данные могут быть описаны обоими видами распределений или вид распределения неопределенный, дальнейшую обработку проводят как для логарифмически-нормального распределения. 9 Определяют ресурсы. 9.1 Определяют среднелогарифмический ресурс (грамматическое ожидание логарифма ресурса) при требуемой температуре
9.2. Определяют средний ресурс при требуемой температуре
9.3 Определяют среднее значение (математическое ожидание) гамма-процентных ресурсов: 9.3.1. Для логарифмически-нормального распределения отказов. 9.3.1.1. Определяют uy математическое ожидание логарифма гамма-процентного ресурса, соответствующее требуемой вероятности безотказной работы по формуле
где uy - квантиль нормированного нормального распределения, определенная для требуемой вероятности безотказной работы (для требуемой величины у). 9.3.1.2. Определяют математическое ожидание гамма-процентного ресурса
9.3.1.3. Для распределения Вейбулла.
где b - параметр формы распределения Вейбулла, определяемый по таблице 3 для коэффициента вариации vb, определяемого по формуле:
10. Определяют нижние доверительные границы для ресурсов. 10.1. Определяют нижнюю доверительную границу средне-логарифмических значений ресурсов при заданной доверительной вероятности Р* (или уровне значимости a = 1 – Р*).
где up* - нижняя доверительная граница средне-логарифмического ресурса при заданной доверительной вероятности; t - распределение доверительных отклонений в малой выборке (распределение Стьюдента), определяемое по статистическим таблицам для за данного уровня доверительной вероятности Р* (например ГОСТ 2126 - 75, приложение 8) и числа степеней свободы fs ;
10.2. Определяют нижнюю доверительную границу среднего ресурса L -при заданной доверительной вероятности Р* как антилогарифм up* Lp* =10up* (27) Таблица 3
103. Для логарифмически нормального распределения определяют up -логарифм ресурса, соответствующий требуемой вероятности безотказной работы, при заданной доверительной вероятности Р* (нижнюю логарифмическую доверительную границу для ресурса при заданной доверительной вероятности Р* и заданной вероятности безотказной работы Р).
где ua - квантиль нормированного нормального распределения, определенная для требуемой вероятности безотказной работы Р (см., например ГОСТ 21126-75, приложение 8); zр - квантиль удвоенной нормированной функции Лапласа, определенная для требуемой доверительной вероятности Р*. 10.4. Для логарифмически нормального распределения определяют нижнюю границу гамма-процентного ресурса при заданной доверительной вероятности Р*.
105. Для распределения Вейбулла определяют нижнюю границу гамма-процентного ресурса при заданной доверительной вероятности Р*.
|
| ОТДЕЛ 1.4 ФГУ ВНИИПО МЧС РОССИИ Материалы сборника могут быть использованы только с разрешения ФГУ ВНИИПО МЧС РОССИИ |

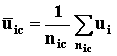 (4)
(4)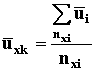 (5)
(5)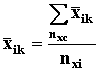 (6)
(6)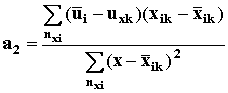 (7)
(7)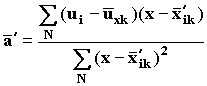 (9)
(9)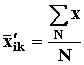 (10)
(10)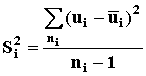 (12)
(12)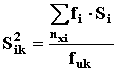 (13)
(13)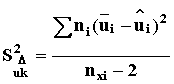 (15)
(15)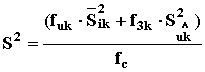 (16)
(16)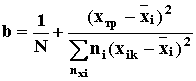 (18)
(18)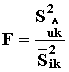 (19)
(19)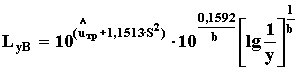 (24)
(24)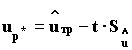 (26)
(26)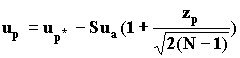 (28)
(28)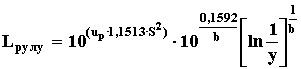 .(29)
.(29)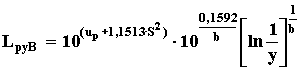 (30)
(30)
Комментарии ()