ГОСТ 10518-88 (Приложение 6)
| ПРИЛОЖЕНИЕ6 (Справочное) ПРИМЕР РАСЧЕТА ПОКАЗАТЕЛЕЙ НАГРЕВОСТОЙКОСТИ Для примера использованы данные испытаний в макетах витковой изоляции с проводом ПЭТД-180 диаметром 1,18 мм и пропиточным лаком УР-9144. Испытания проведены при температурах 180, 200 и 220 °С с длительностью циклов соответственно 17, 6 и 2 сут. Обработка экспериментальных данных проводилась по формулам приложения 4, пункты приложения приведены ниже в скобках. 1. Определение среднелогарифмического ресурса ` ui (пп. 3 и 5) и его дисперcиb S2i (п. 6.1) для каждого испытательного режима. Исходные данные и результаты вычислений приведены в табл. 5-7. При каждой температуре испытаний получено 20 значений. Однако при температуре 180 oС одно значение, равное 1836 ч, исключено (п. 4) в соответствии с приложением 5, так как
Поэтому при температуре 180 °С для вычислений осталось 19 значений. Таблица 5 Определение ` u1 и S12 для Т = 453 К (180 °С)
S n = ni = 19 S uin = 3,63185· 1+3,70757·4+3,74099·1+3,80099·3+3,82814·8 +3,85370·1+3,85783·1 = 71,96274
a (ui–u1)2n=0,02423·1 +3,00639·4+0.00216·1+0,00018·3+0,00165·8+ +0,00438·1+0,00816·1=0,07823
Таблица 6 Определение ` u2 и S22 , для Т = 473 К (200 °С)
a n = ni = 20 a ui = 63,15496 a (ui – ` u1)n = 0,044923
Таблица 7 Определение ` u3 и S32 для Т = 493 К (220 °С)
a n = ni = 20 a uin = 53,06905 a (ui – ` u2)2n = 0,0938
2. Определение коэффициентов линии регрессии (формула 3) п. 5 Промежуточные данные для расчета приведены в табл. 8 и 9. Таблица 8
a = 16,0478·10-9 Таблица 9
1=101,712·10-6 По формуле (7) определяем
По формуле (8) определяем a1 = 3,19957 - 6338·2,1167·10-3 = -10,21608 3. Проверка гипотезы однородности дисперсий (п. 6.3). Определяем средневзвешенную дисперсию ` Sik2 экспериментальных точек относительно средних для них значений ` ui (п 6.2) по формуле (13)
Вычисляем критерий Бартлета (п. 6.3) Полученное значение Б = 2,0 меньше табличного l 2таб = 6,0. Поэтому дисперсии однородны. 4. Проверка гипотезы линейности (п.7). Определяем средние значения ` ui на линии регрессии для испытательных температур xi (п. 6.4) из выражения (формула 20).
Вычисляем дисперсию средних значений относительно соответствующих линий регрессии
Вычисляем дисперсионное отношение F
Условие линейности выполняется для уровня значимости, равного 0,025, так как 5,08 меньше табличного значения, равного 5,29. 5. Определение вида статистического распределения. По критерию w 2 получено в соответствии с ГОСТ 11.006-74, что эмпирические данные могут быть описаны как логарифмически нормальным распределением, так и распределением Вейбулла. 6. Определение среднего ресурса при требуемой температуре tтр =155°C (пп. 9.1 и 9.2). По формулам (20 и 21) определяем
7. Определение среднего значения гамма-процентного ресурса для логарифмически нормального распределения (п. 9.3.1). Определяем общую дисперсию (п. 6.5) по формуле (16).
S = 0,065078 Определяем uy (п. 9.5.1.1) по формуле (22) для - у=0,9 ua =1,282 для у = 0,9 (по таблицам) uy = u0,9 = 4,59233 – 0,065078·1,282 = 4,512154 Определяем математическое ожидание гамма-процентного ресурса (п 9.3.1.2) для у = 0,9 по формуле (23). L0,9 = 10 (4,512154 + 1,1513·0,004235) = 32887 ч » 33000 ч. 8. Определение среднего значения гамма-процентного ресурса для распределения Вейбулла (п. 9.3.2). Определяем коэффициент вариации по формуле (25).
По таблице 3 для vв = 0,1507 параметр формы b распределения Вейбулла равен 7,85. Определяем математическое ожидание гамма-процентного ресурса по формуле (24) для y = 0,9.
9. Определение нижних доверительных границ для ресурсов. Заданная доверительная вероятность Р* = 90 %. Определяем дисперсию средних значений линии регрессии (п. 6.6) для требуемой температуры по формулам (17) и (18)
Определяем нижнюю доверительную границу среднелогарифмического ресурса для 90%-ной доверительной вероятности по формуле (26) uр* = 4,59233 - 1,67·0,02693 = 4,54736. Определяем нижнюю доверительную границу среднего ресурса (п. 10.2) по формуле (27). L90* = 104,54736= 35266 ч » 35000 ч. Для логарифмически нормального распределения определяем логарифм ресурса. соответствующий вероятности безотказной работы 0,9 при 90 % доверительной вероятности (п. 10.3) по формуле (28).
Для логарифмически нормального распределения определяв ч нижнюю границу 90%-ного ресурса при 90 %-ной доверительной вероятности (п. 10.4) по формуле (29).
Для распределения Вейбулла определяем нижнюю границу 90 %-ного ресурса при 90%-ной доверительной вероятности по формуле (30).
|
| ОТДЕЛ 1.4 ФГУ ВНИИПО МЧС РОССИИ Материалы сборника могут быть использованы только с разрешения ФГУ ВНИИПО МЧС РОССИИ |

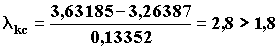
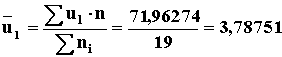
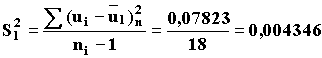
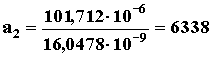
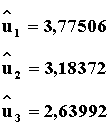
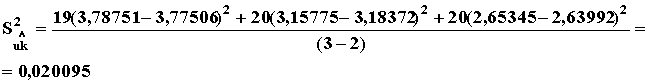
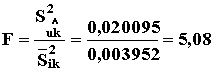
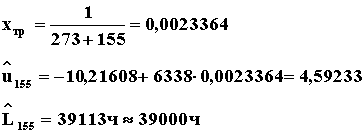
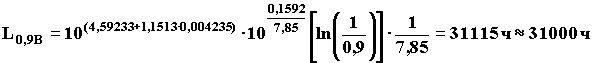
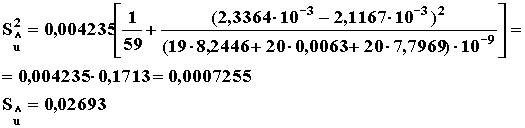
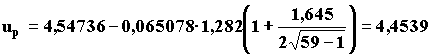
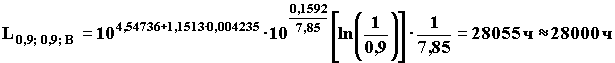
Комментарии ()