ГОСТ 27710-88 (Приложение 2)
| ПРИЛОЖЕНИЕ 2 (Обязательное) РАСЧЕТ ДИАПАЗОНОВ НАГРЕВОСТОЙКОСТИ 1. Область распространения В настоящем приложении даны подробные инструкции по расчету диапазонов нагревостойкости с применением статистических методов. В процессе расчетов статистические переменные сопоставляются с табличными величинами, приведенными в табл. 6 и 7. Примеры охватывают три случая: Пример 1. Непрерывные измерения. Пример 2. Циклическое проведение проверочных испытаний. Пример 3. Разрушающие испытания. 2. Общие положения В основе статистических методов лежат следующие допущения: 1) наблюдаемые величины времени до разрушения образцов стохастически независимы. Образцы для испытания на старение выбирают произвольно из исследуемого множества и обрабатывают одинаково; 2) логарифм времени до разрушения образцов имеет нормальное распределение с одинаковой дисперсией при всех температурах; 3) логарифм времени до разрушения образцов линейно зависит от величины обратной термодинамической температуры старения (уравнение Аррениуса), по крайней мере, во всем диапазоне, включающем все испытательные и экстраполируемые точки; 4) температура старения имеет незначительную погрешность и одинакова для всех образцов, одновременно подвергающихся тепловому воздействию. 3. Методы и результаты испытаний Чтобы определить диапазон нагревостойкости (ДН) электроизоляционного материала в соответствии с заданным критерием конечной точки, необходимо определенное количество образцов подвергнуть циклически или непрерывно воздействию каждой из серии выбранных температур и определить время до разрушения образцов при каждой температуре. Температуры выбирают согласно требованиям данного стандарта. Способ определения времени до разрушения, когда проверяемая характеристика достигнет уровня критерия конечной точки, зависит от метода испытания. 3.1. Повторяющиеся испытания Каждый образец периодически испытывают во время старения либо путем непрерывного измерения проверяемой характеристики, либо путем применения определенного контрольного воздействия в определенные периоды времени. Если проверяемую характеристику измеряют непрерывно, время до разрушения каждого образца получают непосредственно из измерений в виде времени, за которое эта характеристика достигает критерия конечной точки. Это относится ко всем случаям, когда характеристику измеряют непрерывно или достаточно часто во время старения путем испытания без разрушения образцов. Если характеристику измеряют через определенные интервалы времени старения, то зависимость этой характеристики свойства (или некоторой функции ее) от времени (или функции времени) старения изображают графически. Время до разрушения каждого образца определяют по графику, как время, за которое характеристика этого образца достигает уровня критерия конечной точки. Эта методика применима при непрерывном и циклическом старении, когда характеристику определяют с помощью неразрушающих измерений через длительные интервалы времени (например, в конце циклов старения). В некоторых случаях достаточно принять критерий конечной точки за контрольную величину и использовать методику, описанную ниже. Если контрольное испытание проводят через определенные периоды времени старения, то время до разрушения каждого образца определяют как среднее из двух значений времени старения, после которого образец впервые не выдерживает проверочного испытания, и времени старения до непосредственно предшествующего разрушения контрольного испытания, то есть за время до разрушения принимают среднюю точку последнего цикла, воздействию которого подвергают образец. Эту методику применяют в циклических испытаниях, когда все образцы в конце каждого цикла подвергаются контрольным испытаниям, после чего проходят новые циклы и так до тех пор, пока значение проверяемой характеристики не достигнет уровня критерия конечной точки. 3.2. Однократное измерение на каждом образце В этом случае строят график зависимости характеристики от времени старения для каждой температуры и проводят линию наилучшего совпадения со всеми экспериментальными точками в четырех сроках старения, после которых, когда результаты испытаний близки к точке пересечения линии наилучшего совпадения с линией критерия конечной точки, через точки, соответствующие результатам испытаний отдельных образцов, проводят линии, параллельные линии наилучшего совпадения. Абсциссы точек пересечения этих линий с линией критерия конечной точки принимаются за пределы времени до разрушения образцов. Эта методика используется в тех случаях, когда проверяемую характеристику определяют методом разрушающих испытаний и в случаях непрерывного старения, когда после фиксированного периода времени из термостата извлекают определенное количество образцов и после измерения выбрасывают. 4. Статистические расчеты и решения Для каждого значения температуры воздействия J i в °С, при которой проводят старение (i=l, 2 ... , k при k 3), вычисляют: величину, обратную термодинамической температуре (xi ) по формуле
десятичный логарифм (Бригга) времени до разрушения образца (yi) по формуле
где tig -время до разрушения образца номер j, при температуре Ji для j = 1, 2…, ni, где ni - количество образцов, подвергаемых старению при Ji. Общее количество образцов равно N= Sni. 4.1. Проверка равенства дисперсий yig Вычисляют дисперсию (Sij2)при различных величинах xi по формуле
где fi=ni-1 - число степеней свободы S1i2, и суммарную дисперсию (S12) по формуле
а соответствующее число степеней свободы (fi) по формуле f1= Sfi=N-k, Дисперсии сравнивают по методу Бартлетта. Вычисляют промежуточную постоянную (с) по формуле
и стохастическую переменную распределения (c2) по формуле
Переменную c2 сравнивают с ее 0,95 квантилей распределений c2 (0.95, k-1). Если c2>c2(0,95, k-1), величину c2 вносят в протокол вместе с диапазоном нагревостойкости. 4.2 Определение коэффициентов регрессии. Исходя из общего уравнения регрессии Y=а+bх, (8) и из определений взвешенного среднего значения xi
выборочного среднего значения yi
и, следовательно, суммарною среднего значения yij
определяются коэффициенты уравнения регрессии по формулам:
и
Линию регрессии вычерчивают на графике срока службы. 4.3. Проверка линейности Вычисляют дисперсию около линии регрессии по формуле
где f2=k-2 - число степеней свободы s22, и стохастическую переменную в распределении Фишера из формулы
Переменную величину F сравнивают с 0,95 квантилей распределений F (0,95, fn, fd) (табл. 7). Если F>F (0,95, fn, fd) величину F вносят в протокол вместе с диапазоном нагревостойкости. Суммарную оценку дисперсии (s2) вычисляют по формуле
где f=N-2 - число степеней свободы s2. 4.4. Доверительная граница для Y Для выбранных величин Х определяют из уравнения (8) значения Y Y=a+bX (17). и ее дисперсию
Определяют t=t(0,95, f) из табл. 6 и вычисляют нижнюю одностороннюю границу доверительного интервала (Yс) для у по формуле Yc=Y-tsy, (19) где sy есть квадратный корень из дисперсии sy2 Взаимно связанные величины Х и Yc наносят на график срока службы (см. п. 42) и проводят кривую, образующую нижнюю одностороннюю границу доверительного интервала с вероятностью 95 % для истинного значения Y при данной величине X. 4.5. Коэффициент вариации. Из уравнения регрессии вычисляют величину Х5 соответствующую Y5=3,7 (время до разрушения, равное 5000 ч)
и соответствующую дисперсию для Y5
Если коэффициент вариации Сv, в процентах, определяемый из формулы
больше 1,5%, вычисления прекращают и строят только график сроков службы. 4.6. Определение температур, соответствующих времени 20000ч (J20) и 5000 ч (J5) до разрушения образца Применяя формулы (2) и (8) вычисляют
4.7. Определение доверительной границы для J5. Вычисляют промежуточную постоянную br
и ее дисперсию sr2
и находят верхнюю одностороннюю границу для Х
t=t(0,95, f) и находят нижнюю одностороннюю границу доверительного интервала с вероятностью 95 % для J5.
4.8. Диапазон нагревостойкости Диапазон нагревостойкости записывают в соответствии с требованиями п. 7.3.2:
5. Примеры расчета диапазона нагревостойкости Примеры расчетов, которые выполняют последовательно на простом настольном калькуляторе или с помощью логарифмической линейки и таблицы логарифмов. Для удобства используют следующие сокращения:
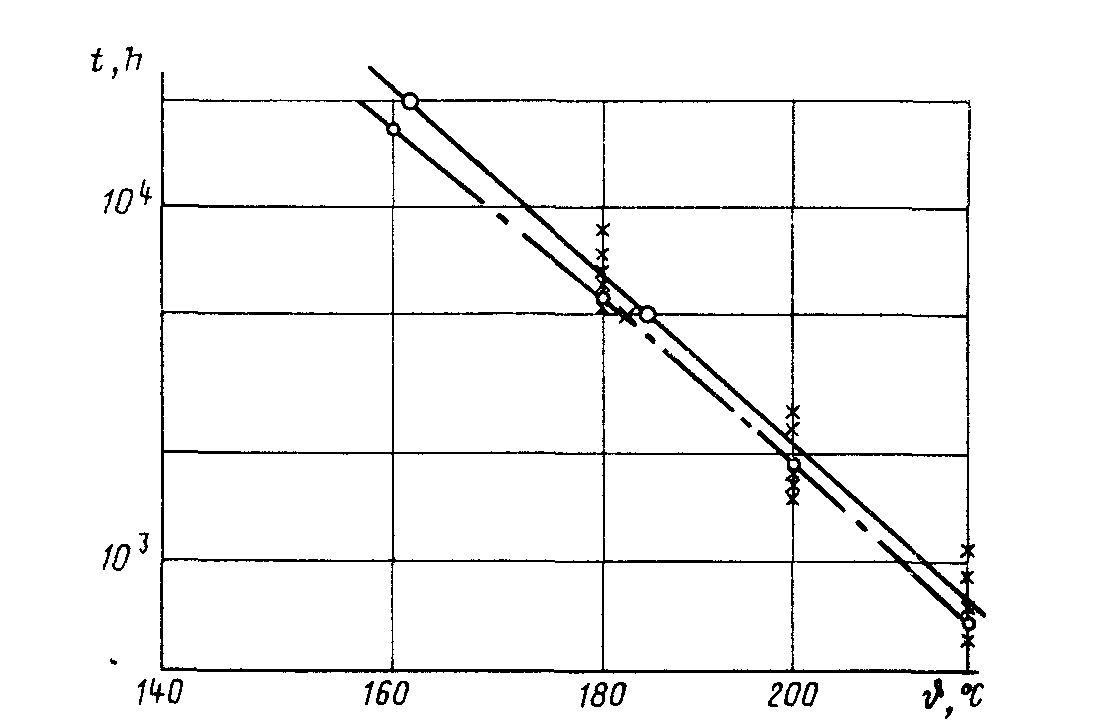
Например, SQD обозначает сумму квадратов разностей. Индексы помещают в скобки. Условные обозначения использованы в таблицах. 5.1. Пример 1 (Непрерывные измерения) Материал испытывают путем непрерывного измерения проверяемой характеристики (например, сопротивление изоляции). Время до разрушения определяют для каждого образца как время старения, после которого сопротивление изоляции снижается до уровня нормированной величины (критерия конечной точки). Предполагаемый температурный диапазон, соответствующий экстраполированному времени до выхода из строя порядка 20 000 ч, составляет от 160 до 169°С. Из табл. 1 выбирают три температуры воздействия: 220, 200 и 180°С, то есть k=3 (i=l; 2; 3). Готовят не менее 15 образцов (N=15) и по 5 из этих образцов, выбранных произвольно, подвергают старению при каждой температуре ni=5 (j=1, 2, 3, 4, 5). Время до разрушения tij , ч приведено в табл. 4, где показан также расчет величины, обратной термодинамической температуре xi и величин yij=lgtij. Для удобства величины х умножают на 1000. В табл. 5 показаны этапы расчета диапазона нагревостойкости. 5.1.1. Дисперсии s21t вычисляют в соответствии с номером этапа (14) V(1, i) с f(i)=4 степенями свободы, суммарную дисперсию s21 в соответствии с номером этапа (26), V(1) с f(i)==12 степенями свободы. Исследуемую переменную c2=0,17, номер этапа (34) - сравнивают с c2 (0,95; 2)=6,0 номер шага (35), полученным из табл. 6. Так как c2<c (0,95; 2), величина c2 не значима на 5%-ном уровне значимости. 5.1.2. Вычисляются коэффициенты регрессии а = - 7,604, номер этапа (53), и b = 5,174, этап (51). Линию регрессии у = - 7,604+5,174x вычерчивают на графике сроков службы (черт. 4). 5.1.3. Сопоставляют исследуемую переменную F = 0,7, номер этапа (63) с F(0,95;1; 12) = 4,8, номер этапа (64). Так как F- F(0,95; 1; 12), величина F не значима на 5 %-ном уровне значимости. 5.1.4. Выбирают температуру 220, 200, 180 и 160°С, этап (70), определяют границу доверительного интервала с вероятностью 95% tc , номер этапа (83), для соответствующих величин t номер этапа (84), с коэффициентом Стьюдента f(0,95; 13) = 1,77, номер этапа (69), и наносят на график службы. Таблица 4
В табл. 6 и 7 даны величины c2 (0,95; f), t (0,95; f) и F (0,95, fn, fd), где fn есть количество степеней свободы числителя и fd - знаменателя в выражении 5.1.5. Вычисляют коэффициент вариации Сv = 0,9%, этап (97). Так как коэффициент вариации Сv< 1,5 % вычисления продолжают. 5.1.6. Величины J5=185°C и J20=162°С вычисляют по этапу (90). 5.1.7. Границу доверительного интервала с вероятностью 95% вычисляют по этапу (113): Jc =182°C. 5.1.8. Диапазон нагревостойкости имеет вид ДН: 162/185 (182). 5.2. Пример 2 (Циклическое применение проверочного испытания) Материал подвергается проверочным испытаниям (например, испытанию заданным напряжением в течение 1 мин в соответствии с табл. 3 испытание 11) Предполагаемый температурный диапазон, соответствующий экстраполированному времени до разрушения, равному 20000ч, от 140 до 149 °C. Из табл. 1 выбирают 3 температуры воздействия и соответствующие длительности воздействия этих температур в циклах, как указано в табл. 8. Подготавливают не менее 30 образцов (N=30) и предварительно проводят проверочные испытания. Все неисправные образцы заменяют. По 10 произвольно выбранных образцов подвергают старению при каждой из трех температур, то есть k=3 (i = l, 2, 3) и ni=10(j=l,2…10). График сроков службы
ґ - экспериментальные точки;O - граница длительного интервала с вероятностью 95% для t;---- - линия регрессии; - - - - - граница доверительного интервала с вероятностью 95% для t; O - J5 и J20;ґ - J с.Черт. 4 После каждого нормированного периода теплового воздействия tp, ч образцы вынимают из термостата и проводят проверочные испытания. Образцы, выдержавшие испытание, снова помещают в термостат для следующего цикла, а для разрушившихся образцов регистрируют количество проведенных циклов старения р в соответствии с табл. 8. Время до разрушения определяют как среднюю точку последнего цикла, т е. t =tp(p-0,5) (28) В табл. 9 показан расчет переменных y = lgt и х равной величине обратной термодинамической температуры. Для удобства величины х умножают на 1000. После этого расчеты выполняют, как в примере 1 (см табл. 10, где числа в скобках относятся к соответствующим этапам в табл. 5) 5.3. Пример 3 (Разрушающие испытания) Материалы подвергаются разрушающим испытаниям (например, определяются пределы прочности при растяжении в соответствии с табл. 3, испытание 21). За критерий конечной точки принимают снижение прочности на 50% от начальной величины. На основе имеющегося опыта предполагается, что логарифм показателя предела прочности при растяжении является линейной функцией времени. Таблица 5
Таблица 6
Таблица 7
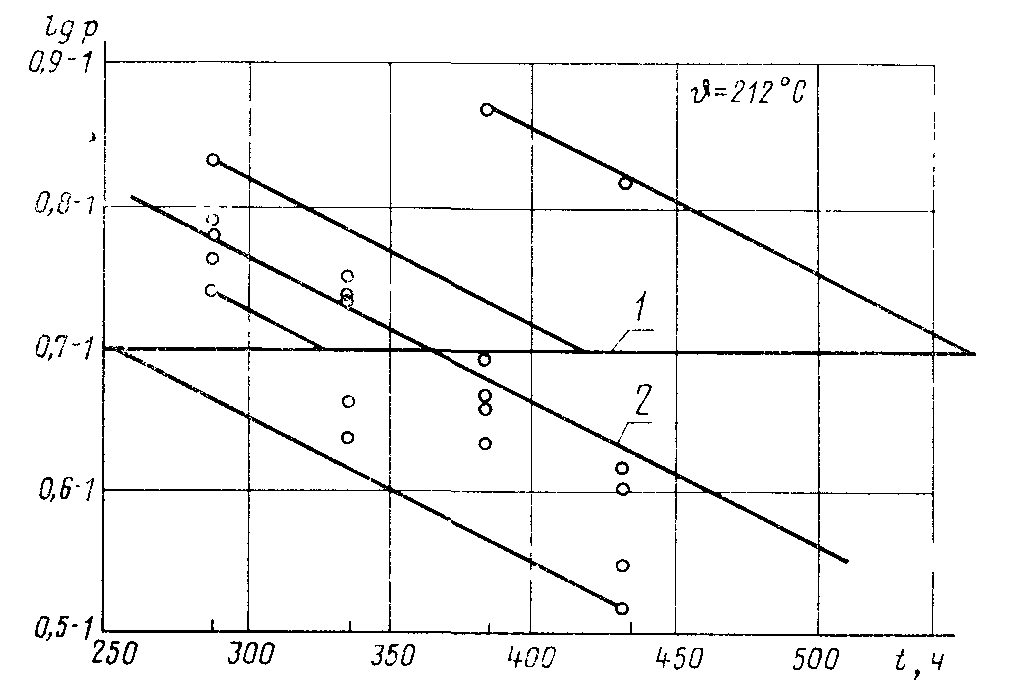
Предполагаемый температурный диапазон, соответствующий экстраполированному времени до разрушения, равному 20000 ч, от 150 до 159 °С. Из табл. 1 выбирают 3 температуры воздействия J°С и периоды воздействия tp =48 при 210°С, 168 ч при 190°С и 672 ч при 170°С. Подготавливают около 200 образцов. 10 образцов, выбранных произвольно, подвергают старению в течение 48 ч при 170°С, после чего их испытывают, чтобы определить начальную величину предела прочности при растяжении. Оставшиеся образцы делят произвольно на три группы в термостатах при температурах 212, 190 и 171 °С. В конце каждого периода старения на 5 образцах определяют предел прочности при растяжении, после чего их выбрасывают. Предел прочности при растяжении выражают в виде lg p - логарифма отношения измеренной величины к начальному значению. Тогда критерий конечной точки принимает вид lg рс = lg 0,5 =0,6990-1. Полученные таким образом величины lg p приведены в табл. 11 для 4 сроков старения, после которых среднее значение измерений величины проверяемой характеристики наиболее близко к критерию конечной точки, как показано на черт. 5, для случая J=212°С. Для более точного построения зависимости изменения проверяемой характеристики от времени старения при каждой из трех температур результаты испытаний обрабатывают по методу наименьших квадратов следующим образом. Рассчитывают коэффициенты в уравнении у=а+bх где y - lg p. х - продолжительность старения до момента измерения tm;
где
а
k=4, количество сроков старения, после которых использованы результаты испытаний для построения графика изменения свойства при каждой температуре (i=l, 2, 3, 4) и ni=5, количество образцов, испытанных после каждого срока старения (j= 1, 2,..., 5). Расчеты приведены в табл. 12. По результатам расчета проводят линию наилучшего совпадения с экспериментальными точками. Для каждого образца через точку, выражающую результат его испытания, проводят линию, параллельную линии наилучшего совпадения, как показан” на черт. 5 для случая J=212 °С. Время, соответствующее точке пересечения линии отдельного образца с линией критерия конечной точки, принимают за время до разрушения этого образца. Время до разрушения образца вычисляют по формуле
где tm - время до момента измерения и lg ре =0,6990-1 - критерий конечной точки. Таблица 8
Таблица 9
Таблица 10
Таблица 11
Определение предлагаемого времени до разрушения образца (разрушающие испытания)
Черт. 5 1-линия критерия конечной точки; 2-линия наилучшего совпадения Таблица 12
То есть, если предположить, что образец испытывается во время t вместо времени tm, то измеренной величиной будет рc вместо фактически измеренной величины р. Полученное таким образом предполагаемое время до разрушения образца fij приведено в табл. 13. Расчет диапазона нагревостойкости продолжают как в примере 1 с тремя температурами (k=3) и 20-ю образцами при каждой температуре ni =4,5=20) с общим числом N=kЧni=60 образцов. Таблица 13
В табл. 14 показан расчет, проведенный на настольном электронном калькуляторе с введенными статистическими программами для определения средней величины, стандартного отклонения и коэффициентов в уравнении регрессии при fi=ni-1=19, fi=kfi=57, f=N-2=58,
Диапазон нагревостойкости определяют как ДН:156/174(173). Таблица 14
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ОТДЕЛ 1.4 ФГУ ВНИИПО МЧС РОССИИ Материалы сборника могут быть использованы только с разрешения ФГУ ВНИИПО МЧС РОССИИ |

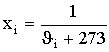 , (2)
, (2)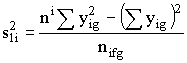 , (4)
, (4)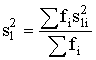 , (5)
, (5)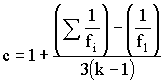 , (6)
, (6)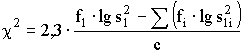 , (7)
, (7)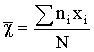 , (9)
, (9)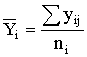 , (10)
, (10)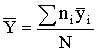 , (11)
, (11)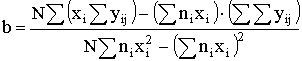 , (12)
, (12)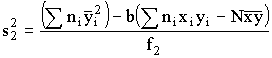 , (14)
, (14)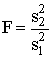 , (15)
, (15)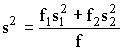 , (16)
, (16)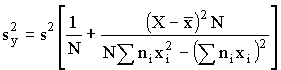 , (18)
, (18)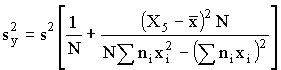 , (21)
, (21)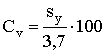 , (22)
, (22)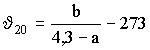 , (23)
, (23)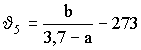 , (24)
, (24)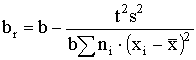 , (25)
, (25)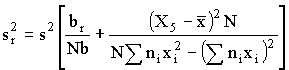 , (26)
, (26)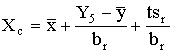 , (27)
, (27)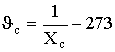 .
.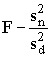 .
.
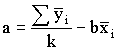 , (29)
, (29)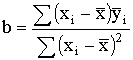 , (30)
, (30)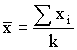
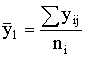
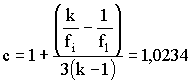 .
.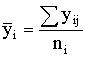
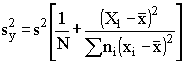
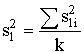
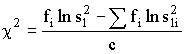
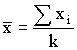
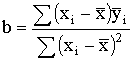
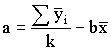
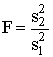
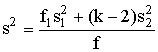
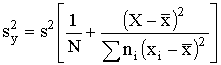
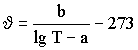
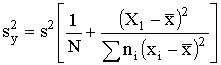
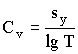
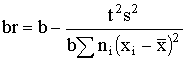
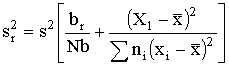
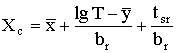
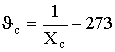
Комментарии ()